1. INTRODUÇÃO

            Uma das características do pensamento humano é lidar com situações de ambigüidade, incerteza e informações vagas na resolução de problemas, que usa o conhecimento adquirido com diversas situações do cotidiano e sua intuição, para lidar com a mesma.

            Nesse tipo de problemas, de difícil solução, em que se faz necessário o auxílio matemático computacional, a modelagem de tais fatores é extremamente complicado. Portanto, impossíveis de serem caracterizadas por predicados da lógica clássica bivalente.          

            Desenvolvido por Lotfi Zadeh, a Lógica Fuzzy veio para suprir essa necessidade, permitindo tratar matematicamente os níveis de incerteza e ambigüidade.

A lógica difusa, como também é conhecida, vem tornando possível cada vez mais aproximar a máquina ao raciocínio humano. E propondo soluções cada vez mais realistas a problemas que antes só o cérebro humano era capaz de interpretar e resolver.

2. LÓGÍCA FUZZY

2.2. O que é a Lógica Fuzzy?

O termo fuzzy significa nebuloso, difuso, algo que não está claro, e se refere ao fato de, em muitos casos, não conhecermos completamente os sistemas que estamos analisando. Em muitos problemas em física e matemática, nós não temos dificuldade em classificar elementos como pertencentes ou não a um dado conjunto clássico. Dessa forma, dado um conjunto A e um elemento x do conjunto universo U conseguimos muitas vezes dizer se   ou .

Podemos, por exemplo, afirmar sem receio que o número e que . Este é um caso sobre o qual não se tem dúvida, sendo a lógica booleana perfeitamente aplicável. No entanto, podemos discordar quanto ao fato de 6,5 pertencer ou não ao conjunto dos números aproximadamente iguais a 7. Neste caso a resposta não é única e objetiva, pertencer ou não vai depender do tipo de problema que estamos analisando.

Para ilustramos esta situação, suponhamos que um aluno obteve média 6,5. O professor nessa situação poderá analisar o caso levando em consideração a capacidade do aluno, a sua dedicação durante o curso. E pode decidir pela aprovação do aluno mesmo não tendo atingido a média 7. Note que, neste caso, o número 6,5 está sendo considerado como pertencente ao conjunto dos aproximadamente iguais a 7.

Existem inúmeras situações em que a relação de pertinência não está bem definida, e nestes casos, não sabemos dizer se o elemento pertence ou não a um determinado conjunto. A intenção de Zadeh foi justamente trabalhar de forma a flexibilizar a pertinência de elementos aos conjuntos, criando uma idéia de grau de pertinência. Podendo, assim, um determinado elemento pertencer parcialmente a um conjunto. Esta idéia foi publicada por Zadeh em 1965, ano que pode ser considerado o marco do nascimento da teoria dos conjuntos fuzzy.

Se desejarmos, por exemplo, construir o conjunto dos números aproximadamente iguais a 5, citado acima, como deveríamos proceder? Será que os números 2 e 10 pertenceriam a este conjunto? Claramente esta resposta dependeria do contexto.

O que Zadeh nos propõe é considerarmos uma função que nos forneça o quanto um determinado número pertence ao conjunto considerado. Sendo assim, chamando de K o conjunto dos números aproximadamente iguais a 5, no universo dos números naturais N, podemos propor por exemplo uma função de pertinência onde:

Esta extensão da função característica da lógica clássica para o intervalo [0,1], originou os conjuntos fuzzy e possibilitou, entre outras coisas, a utilização de variáveis lingüísticas, permitindo a exploração do conhecimento humano no desenvolvimento de vários sistemas.

A figura abaixo, apresenta a função de pertinência de um conjunto fuzzy que corresponde aos números aproximadamente iguais a cinco. Note que nesse caso a função de pertinência é discreta, mas também pode ser contínua.

Lógica Difusa ou Lógica Nebulosa, também pode ser definida, como a lógica que suporta os modos de raciocínio que são aproximados, ao invés de exatos, como estamos naturalmente acostumados a trabalhar. Ela está baseada na teoria dos conjuntos nebulosos e difere dos sistemas lógicos tradicionais em suas características e detalhes. Nesta lógica, o raciocínio exato corresponde a um caso limite do raciocínio aproximado, sendo interpretado como um processo de composição nebulosa.

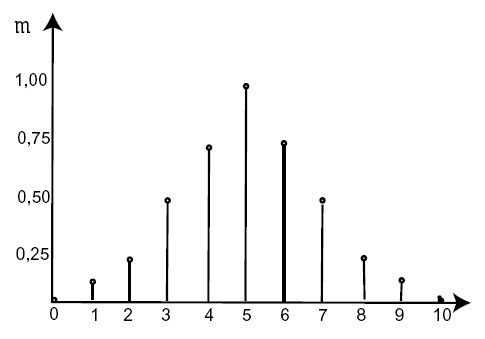
Figura 1: Números aproximadamente iguais a 5

2.1. Por que Lógica Fuzzy?

No mundo real usamos palavras como: muito, pouco, grande, pequeno, freqüentemente, raramente, etc. para descrever situações. Estas situações não são nitidamente definidas e não podem ser precisamente descritas. Por exemplo, as frases abaixo são de uso corrente em nossa linguagem, e apesar de transmitirem informações imprecisas elas são usadas em tomadas de decisões:

• O carro está andando muito rápido, pise no freio.
• Ele é uma pessoa muito feliz.
• Esta sala é pequena para todos os alunos, reserve outra maior.
• Nesta cidade a temperatura freqüentemente está alta, gastamos muita energia nos condicionadores de ar.

A descrição completa de um sistema real em muitos casos requer dados extremamente detalhados e muito além do que um ser humano poderia simultaneamente, processar e entender. No entanto, freqüentemente executamos tarefas complexas que para serem descritas necessitam destes termos imprecisos que não podem ser modelados pela matemática tradicional de conjuntos. Podemos citar exemplos simples, que encontramos no nosso dia

a dia.

• Preparar alguns pratos a partir de receitas.
• Estacionar um carro.
• Controlar uma carteira de investimentos.

Nessas atividades, especialistas usariam frases como:

• Coloque no forno até ficar no ponto.
• Vire o volante um pouco para a direita.
• Se a taxa de juros subir muito e o déficit for alto, teremos uma recessão branda.
• Se estivermos na hora o rush, aumente muito a freqüência de trens.
• Se temos muita roupa suja na máquina de lavar, aumente o tempo de lavagem.
• Se a terra está muito seca e temperatura está alta, regue durante muito tempo.

Daí a necessidade de se fazer um estudo sobre como lidar com ambigüidades, incerteza e informações vagas na resolução de problemas em que se faz necessário o auxílio matemático computacional.

2.3. Lógica Booleana X Teoria da Lógica Fuzzy

A lógica de Aristóteles estabelece um conjunto de regras rígidas para que as conclusões sejam aceitas como lógicas válidas; seguindo uma linha de raciocínio baseada em premissas e conclusões. Como por exemplo:

“Todo ser vivo é mortal" (premissa 1)

“João é um ser vivo" (premissa 2),

Como conclusão temos:

“João é mortal".

Esta lógica formal é considerada binária, pois uma declaração é falsa ou verdadeira, não podendo ser ao mesmo tempo parcialmente verdadeira e parcialmente falsa. Obrigatoriamente, uma declaração deve fazer parte de apenas um conjunto, o das declarações verdadeiras ou o das declarações falsas. Esta suposição é o Princípio da Não-Contradição, que coloca A e não A cobrindo todas as possibilidades, sendo considerada a base do pensamento lógico tradicional.

A Lógica Fuzzy viola estas suposições. O conceito de dualidade estabelece que algo pode e deve coexistir com o seu oposto; o que faz a Lógica Fuzzy parecer natural e até mesmo inevitável. A lógica booleana trata com valores “verdade" das afirmações, classificando-as como verdadeiras ou falsas. Mas, muitas das experiências humanas não podem ser classificadas simplesmente como verdadeiras ou falsas, sim ou não, branco ou preto. Por exemplo, é aquele homem alto ou baixo? A taxa de risco para aquele empreendimento é grande ou pequena? Um sim ou um não como resposta a estas questões é, na maioria das vezes, incompleta. Na verdade, entre a certeza de ser e a certeza de não ser, existem infinitos graus de incerteza. Ao contrário da lógica booleana, a lógica fuzzy não impõe limites bruscos, mas proporciona graus de pertinência de elementos a uma determinada categoria.

Para exemplificar, utilizaremos à palavra meia-idade. É comum classificarmos uma pessoa de meia idade ou não, apesar de não se saber exatamente quando começa e termina esse período. Vamos assumir que o período vai de 35 a 55 anos. Pela lógica tradicional, uma pessoa de 34 anos só pertenceria ao grupo de meia-idade depois de dia de seu aniversário de 35 anos. Da mesma maneira, uma pessoa de 56 anos não pertenceria mais a este grupo. A figura abaixo mostra a definição de meia idade segundo a lógica convencional:

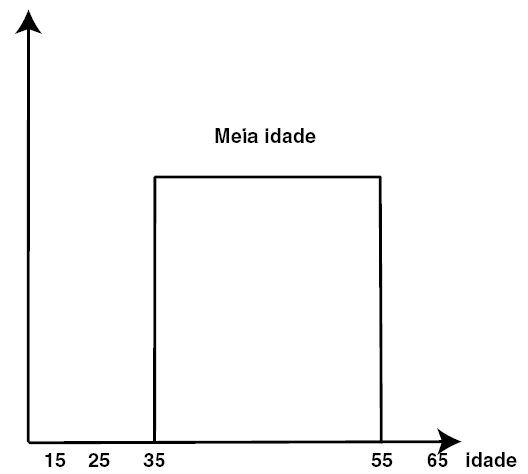
Figura 2: Definição conjuntos convencionais de meia idade

Mas não é desejada tamanha precisão em relação a este conceito, pois o limite de meia-idade não pode ser definido precisamente. Note que os limites do conjunto acima são muito rígidos. O ideal é ter limites graduais, onde são associados graus de certeza que uma pessoa seria ou não de meia idade. A figura 3 mostra a definição de meia-idade segundo a lógica fuzzy:

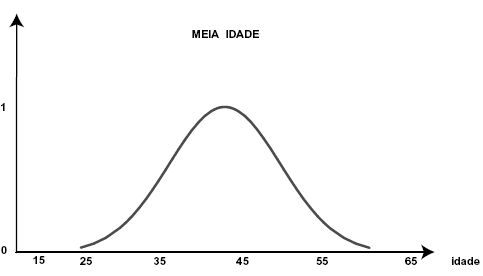
Figura 3: Definição fuzzy de meia idade

3. TEORIA DE CONJUNTOS FUZZY

Na teoria clássica dos conjuntos, há uma rigidez de tal forma que um dado elemento do universo em discurso (domínio) pertence ou não pertence ao referido conjunto. Na teoria dos conjuntos nebulosos existe um grau de pertinência de cada elemento a um determinado conjunto. Este conceito parece ser bastante natural e facilmente percebido ao examinarmos a lista de conjuntos abaixo:

·        Conjunto dos números naturais (I)

·        Conjunto dos números inteiros (I)

·        Conjunto dos números naturais aproximadamente iguais a sete (II)

·        Conjunto dos clientes com alta renda (II)

·        Conjunto dos homens altos (II)

Observando os exemplos acima, percebe-se claramente que existe uma diferença fundamental entre os conjuntos do tipo (I) e os conjuntos do tipo (II). Por exemplo, apresentado um número podemos afirmar sem nenhuma discussão ou dúvida se esse número pertence ou não pertence ao conjunto dos números inteiros.

Esta questão não é tão simples quando lidamos, por exemplo, com o conjunto dos homens altos. Uma pessoa que tenha 1,74 metros de altura, seria considerada como pertencente a esse conjunto? E a de 1,75? Tomando como padrões a definição de homem alto pela medida maior ou igual a 1,80, mediano pela medida 1,70 e baixo pela medida 1,60, veremos claramente na figura 4 que não existe uma fronteira bem definida que separe os elementos do conjunto dos homens altos dos elementos do conjunto dos homens não altos.

Os conjuntos fuzzy são conjuntos que não possuem fronteiras bem definidas e que foram introduzidas devido ao fato de os conjuntos clássicos apresentarem limitações para lidar com problemas onde a transição de uma classe para outra deve acontecer de forma suave.

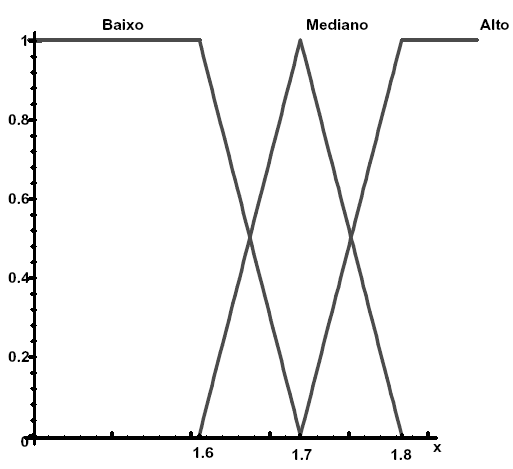
Figura 4: Estatura.

4.1 FUNÇÃO DE PERTINÊNCIA

A função de pertinência mostra o grau de pertinência de um elemento em relação a um determinado conjunto. Também chamada de função característica, ela associa cada elemento x pertencente a U um número real  no intervalo [0 , 1]. Este valor representa o grau de possibilidade de que o elemento x venha a pertencer ao conjunto A, isto é, o quanto é possível para o elemento x pertencer ao conjunto A.

Sua definição, propriedades e operações são obtidas a partir da generalização da teoria dos conjuntos clássicos. Observamos que os conjuntos clássicos são um caso particular da teoria de conjuntos fuzzy. A teoria dos conjuntos clássicos está baseada na função característica clássica, dada por:

onde U é o conjunto universo, A é um subconjunto de U e x é um elemento de U, ou seja, a função característica é um mapeamento do conjunto universo no conjunto {0,1}.

Essa função característica, discrimina entre todos os elementos de U aqueles que, segundo algum critério, pertencem ao subconjunto A, dividindo o conjunto universo em duas partes com fronteiras bem definidas.

Para obtermos os conjuntos fuzzy e suas operações basta generalizarmos a função característica da lógica clássica para o intervalo [0; 1], ou seja, , o que implica em considerarmos um contínuo de valores de pertinência e não apenas pertence e não pertence. O elemento x pertenceria ao subconjunto A com um grau de pertinência que é um valor no intervalo [0,1].

Definição: Um conjunto fuzzy A em um conjunto universo U é um conjunto de pares ordenados de um elemento genérico x e seu grau de pertinência da forma:

4.2 Variáveis Lingüísticas

Além da função de pertinência, há um outro conceito bastante importante relacionado com conjuntos nebulosos, que é o de variável lingüística. Entende-se por variável um identificador que pode assumir um dentre vários valores. Deste modo, uma variável lingüística pode assumir um valor lingüístico dentre vários outros em um conjunto de termos lingüísticos. Estas variáveis têm seu valor expresso qualitativamente por um termo lingüístico (que fornece conceito à variável) e quantitativamente por uma função de pertinência.

De fato, uma variável lingüística é caracterizada por n, T, X, m(n) onde n é o nome da variável (por exemplo, temperatura, pressão, febre, etc.), T é o conjunto de termos lingüísticos de n (elevado, baixo, pouco, extenso, etc.), X é o domínio (Universo) de valores de n sobre o qual o significado do termo lingüístico é determinado (a febre pode estar, por exemplo, entre 35 e 40ºC ) e m(t) é uma função semântica que assinala para cada termo lingüístico  o seu significado, que é um conjunto fuzzy em X (ou seja,  onde X é o espaço dos conjuntos fuzzy). A figura abaixo mostra um exemplo de variável lingüística. O nome n da variável é Febre.

Os termos lingüísticos  que atribuem um significado semi-quantitativo a Febre são: baixa , média e alta. O domínio X da variável é o intervalo [36, 40]. Cada termo lingüístico tem a ele associado um conjunto fuzzy m(t) que o caracteriza. Note que, na formulação clássica, os termos lingüísticos atribuídos para febre são: presente e ausente.

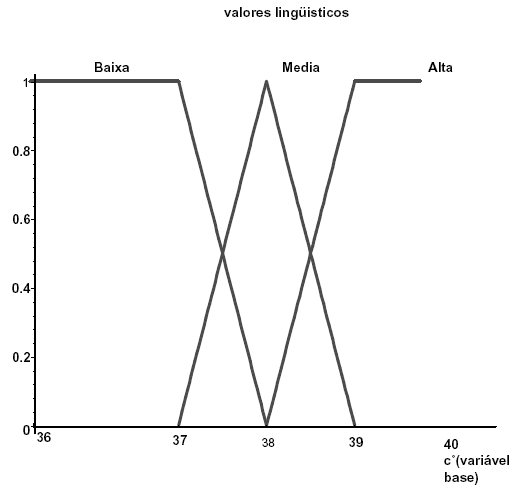
Figura 5: Febre.

As variáveis utilizadas em lógica fuzzy são chamadas de lingüísticas por não terem valores precisos, podendo ser definidas como na linguagem, representando um espectro de valores. Por exemplo, quando dizemos que a temperatura está normal, isso não significa um valor exato, mas um intervalo. Desta forma, definimos as variáveis fuzzy através de conjuntos para representar os intervalos conforme entendemos através das variáveis.

4.3. Operações Fuzzy Básicas

            Suponha três conjuntos fuzzy denominados “pequeno”, “médio” e “grande”, em um universo de discurso real U:[0,5], descritos nas equações representadas em 7.7. Estes conjuntos estão representados na Figura 7.4. A seguir, serão descritas operações fuzzy básicas executadas entre estes conjuntos.